Contoh Soal Distribusi Binomial – Di kelas 12 SMA, terdapat sub materi Distribusi Binomial dari mata pelajaran Matematika. Materi tersebut merupakan salah satu materi dalam ilmu statistik mengenai peluang (probabilitas). Di mana ketika seseorang melakukan percobaan memiliki kemungkinan sukses serta gagal.
Dalam ilmu statistika distrubusi binomial juga dikenal sebagai distribusi Bernouli. Hal ini dikarenakan penemu teori distribusi binomial merupakan matematikawan asal Swiss bernama Jacob Bernauli.
Salah satu ciri utama percobaan Bernauli adalah tidak adanya kontinuitas antara suatu eksperimen dengan eksperimen lain. Artinya jika melakukan 2 (dua) percobaan, maka hasil pertama tidak akan berpengaruh pada hasil percobaan kedua.
Karena materi distribusi binomial cukup kompleks, cara paling mudah untuk mempelajarinya adalah melalui contoh soal. Itulah sebabnya di sini kursiguru akan memberikan uraian seputar distribusi binomial, dari mulai pengertian, rumus, serta penyelesaian soal & jawabannya.
Pengertian Distribusi Binomial
Distribusi binomial merupakan distribusi probabilitas/peluang khusus tipe data diskret (diskontinu), dimana hasilnya selalu bernilai sukses atau gagal saja. Distribusi binomial dapat dipakai saat eksperimennya paling sedikit berjumlah 2 (dua) kali.
Materi mengenai Distribusi Binomial bisa dikaitkan dengan kehidupan sehari-hari. Misalnya saja peluang sukses dan gagal, sehat dan sakit, dan lain sebagainya. Selain itu, dalam permainan dadu juga bisa gunakan teori Dsitribusi Binomial.
Persyaratan Eksperimen Binomial
Agar sebuah percobaan termasuk dalam jenis eksperimen binomial, harus memenuhi beberapa persyaratan, yaitu:
- Jumlah percobaan tetap (fixed number of trial).
- Tiap eksperimen pasti memiliki 2 (dua) hasil, yaitu sukses atau gagal.
- Peluang sukses tiap ekperimen besarnya sama.
- Setiap eksperimen bersifat bebas dan tidak terikat pada eksperimen lain.
Ciri-ciri Distribusi Binomial
Distribusi binomial memiliki beberapa ciri khusus, yaitu:
- Percobaan dilakukan berulang sebanyak n kali.
- Peluang berhasil dinyatakan sebagai p, sedangkan peluang gagal sebagai q, dimana p = 1-q.
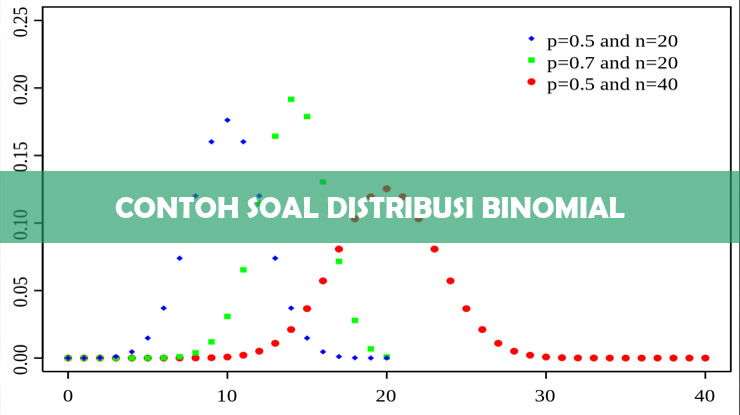
- Jika n tetap serta p kecil atau <0,5, maka distribusinya miring ke kanan.
- Jika p tepat 0,5 distribusi simetris.
- Jika p>0,5 distribusi miring ke kiri.
- Apabila p bernilai tetap, sedangkan n makin besar maka distribusinya mendekati distribusi simetris.
- Keluaran eksperimen hanya memiliki 2 (dua) kategori, contoh: berhasil & gagal, ya & tidak.
- Setiap percobaan memiliki sifat independen (bebas) satu dengan lainnya.
Materi Distribusi Binomial
Perhitungan distribusi binomial pada umumnya dilakukan pada percobaan dengan kemungkinan sukses mulai dari nol mutlak (semua gagal) hingga sukses total (semua sukses).
Dimana jumlah kesuksesan maksimal pada distribusi normal akan bernilai sama dengan besaran n (jumlah eksperimen). Pada soal distribusi binomial normal, besarnya rata-rata (mean) serta varians juga dapat dicari dengan mudah.
Jenis Distribusi Binomial Khusus
Karena dalam beberapa kasus distribusi binomial memiliki faktor penentu yang berbeda dari kondisi normal, maka muncul beberapa jenis distribusi binomial khusus. Jenis distribusi binomial khusus diantaranya adalah:
1. Distribusi Binomial Negatif
Meskipun bernama negatif, bukan berarti hasil perhitungan distribusi binomial ini bernilai minus. Distribusi binomial negatif bukan mencari besarnya kesuksesan sebuah percobaan, melainkan mencari peluang kondisi awal terpenuhi untuk hasil kesuksesan tertentu.
2. Distribusi Binomial Kumulatif
Distribusi binomial kumulatif dikatakan berbeda dari kondisi normal karena akan menghitung besarnya peluang beberapa kondisi sukses sekaligus.
3. Distribusi Binomial Poisson
Distriubsi binomial poisson merupakan jenis paling special. Karena akan digunakan hanya jika besar peluang suksesnya kecil (p<0,05) sedangkan jumlah percobaannya besar (n>20).
Rumus Distribusi Binomial
Berikut adalah persamaan/rumus seluruh jenis distribusi binomial, serta rumus mean dan rumus varian nya.

Dimana khusus untuk rumus distribusi binomial poisson harus mencari besarnya lambda (λ), yaitu λ = n × p.
Contoh Soal Distribusi Binomial dan Jawabannya
Contoh Soal 1
Soal:
Sebuah survei kebersihan gigi memperlihatkan bahwa 2 dari 5 orang sudah pergi ke dokter gigi dalam beberapa bulan terakhir. Apabila ada 12 orang terpilih secara acak, hitunglah probabilitas 4 diantaranya pergi ke dokter dua bulan lalu?
Jawabannya : 0,213
Penyelesaiannya

Contoh Soal 2
Soal:
Berdasarkan contoh soal 1 di atas, tentukanlah besar Mean dan Variannya!
Jawabannya : 4,8 dan 2,88
Penyelesaiannya
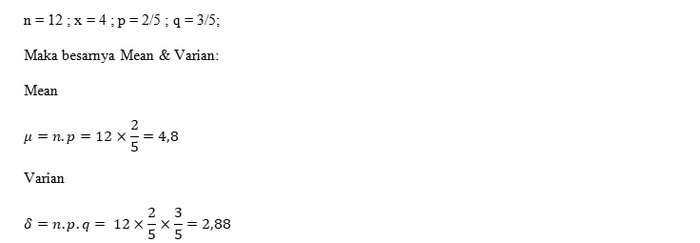
Contoh Soal 3
Soal:
Di sebuah madrasah, ada 5 guru berpartisipasi dalam tes UKG, dimana tingkat kelulusannya sebesar 0,6. Hitunglah probabilitas saat kondisi paling banyak 2 guru lulus! (contoh soal distribusi binomial kumulatif)
Jawabannya : 0,091307
Penyelesaiannya

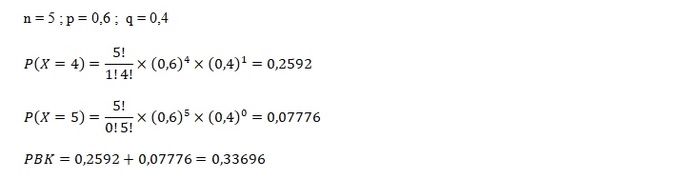
Contoh Soal 4
Soal:
Berdasarkan contoh soal 3 di atas, hitung probabilitas saat kondisinya paling tidak 4 guru lulus!
Jawabannya : 0,33696
Penyelesaiannya
Contoh Soal 5
Soal:
Bertrand Zobrist melakukan eksperimen penelitian Osteoarthritis (OA) terhadap tikus, hingga mendapatkan hasil 4 ekor terserang penyakit OA. Apabila kemungkinan terserang OA adalah sebesar 40%, berapakah peluang Bertrand Zobrist membutuhkan 10 ekor tikus?
Jawabannya : 0,10033
Penyelesaiannya

Contoh Soal 6
Soal:
Berdasar contoh soal 5 terkait distribusi binomial negatif, berapa peluang Bertrand Zobrist memerlukan hanya 6 ekor tikus?
Jawabannya : 0,9216
Penyelesaiannya

Contoh Soal 7
Soal:
Sebuah perusahaan chipset motherboard mampu menghasilkan 1000 unit setiap harinya. Jika data perusahaan menunjukkan 0,5% dari keseluruhan chipset mengalami kerusakan, berapa besar probabilitas 5 chipset rusak dalam satu hari? (Gunakan pendekatan distribusi binomial normal)
Jawabannya : 0,1759
Penyelesaiannya
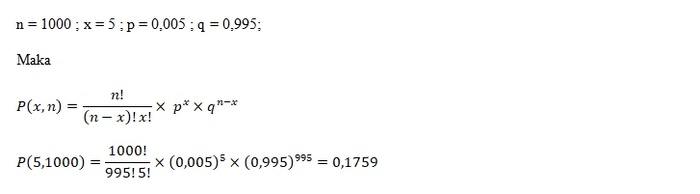
Contoh Soal 8
Soal:
Dari data contoh soal 7 di atas, tentukan besar kemungkinannya melalui rumus distribusi binomial poisson.
Jawabannya : 0,1755
Penyelesaiannya

Contoh Soal 9
Soal:
Di sebuah sekolah, ada 5 siswa berpartisipasi dalam uji coba tes AKM, dimana tingkat kelulusannya sebesar 0,8. Hitunglah probabilitas saat kondisi paling sedikit 3 siswa lolos tes!
Jawabannya : 0,94208
Penyelesaiannya

Contoh Soal 10
Soal:
Berdasarkan contoh soal 9, hitunglah probabilitas saat hasilnya paling sedikit 2 siswa lolos tes AKM!
Jawabannya : 0,99328
Penyelesaiannya

Download Contoh Soal Latihan Distribusi Binomial
Dari beberapa contoh soal di atas, tentunya para siswa kelas 12 sudah punya gambaran dan sedikit memahami materi Distribusi Binomial. Nah, agar pemahaman siswa pada materi bisa sempurna, maka di bawah ini Kursiguru berikan contoh soal latihan lainnya. Kamu bisa download langsung sebagai bahan belajar bersama teman sekelas.
Contoh Soal Distribusi Binomial Lengkap PDF
Akhir Kata
Dengan diberikannya contoh soal dalam bentuk PDF, akhirnya selesai sudah pembahasan kita kali ini. Bisa disimpulkan, bahwasanya dalam memahami dan mengerjakan soal Binomial memang sedikit sulit, akan tetapi jika sudah bisa mengerjakan satu soal tentunya soal-soal berikutnya bisa terselesaikan.
Dalam mempelajari ilmu Matematika, kita perlu tahu beberapa hal. Mulai dari mempelajari trik dan rumusnya, sering belajar bersama, pahami konsep dasarnya, memperbanyak mengerjakan latihan soal, dan mencari suasana tenang ketika mempelajari materi.
Sekiranya itulah uraian seputar contoh soal statistik distribusi binomial dari kursiguru. Berlatih mengerjakan contoh soal distribusi binomial secara mandiri akan lebih membantu memahami ilmu distribusi binomial. Jadi gunakanlah file contoh soal di atas semaksimal mungkin.