Contoh Soal Kesamaan Suku Banyak – membahas mengenai cara mengerjakan soal suku banyak terutama tentang mencari nilai satu atau beberapa sukunya. Dimana suku banyak dapat dicari nilainya asalkan terdapat kesamaan dengan persamaan lain.
Seperti telah diketahui bersama bahwa dalam matematika kelas 11 terdapat sebuah materi berjudul polinomial atau suku banyak. Dimana dalam penyelesaian suku banyak terdapat suatu cara yakni mencari kesamaan.
Contoh soal kesamaan suku banyak sendiri sebenarnya cukup sederhana asalkan kamu sudah memahami bagaimana bentuk dasar penyelesaian persamaan linear. Oleh karena itu, sebaiknya sebelum mendalami soal kesamaan suku banyak pelajari lebih dulu Contoh Soal SPLDV.
Pada kesempatan kali ini, Kursiguru hendak membahas secara spesifik mengenai contoh soal kesamaan suku banyak serta jawaban dan penyelesaiannya. Silakan simak uraian di bawah ini untuk mengetahui gambaran bentuk contoh soal kesamaan suku banyak.
Ringkasan Pembelajaran Kesamaan Suku Banyak
Sebelum menuju ke pembahasan contoh soalnya, mari bahas lebih dulu mengenai gambaran atau rangkuman materi kesamaan suku banyak. Dimana kesamaan suku banyak merupakan sebuah metode penyelesaian dua buah persamaan linear dengan derajat sama.
Sebagai contoh sederhana bentuk px3+qx2+rx+s = ax3+bx2+cx+d dikatakan memiliki kesamaan suku karena derajat p=a; q=b; r=c; serta s=d. Hal itu juga berlaku pada suatu persamaan linear bentuk pembagian.
Umumnya soal kesamaan suku banyak mengharuskan kamu mencari nilai beberapa koefisien dari dua buah persamaan linear. Contoh soal kesamaan suku banyak sederhana : carilah masing-masing a & b berdasarkan x2+4x+2a = 2x2+(a+b)x+12.
Pertama ubah dulu bentuknya agar lebih mudah
x2+4x+2a = 0
2x2+(a+b)x+12 =0
Lalu setarakan menjadi
2x2+8x+4a = 0
2x2+(a+b)x+12 =0
Sehingga diketahui bahwa
(a+b) = 8 -> b=8-a
4a = 12
Kemudian
4a = 12
a = 3
b = 8-a = 8-3 = 5
Contoh Soal Kesamaan Suku Banyak
Agar lebih memahami tentang soal kesamaan suku banyak, simaklah beberapa soal di bawah ini. Dimana contoh soal kesamaan suku banyak berikut telah dilengkapi dengan jawaban serta pembahasan setiap soalnya.
Contoh Soal (1)
Ketika Franky membagi 2x3+ax2-bx+3 dengan (x2-4) menghasilkan sisa pembagian (x+23). Carilah hasil pengurangan (a-b) nya.
A. 2
B. -2
C. 12
D. -12
Jawaban : B. 2
Pembahasan :
Karena diketahui hasil pembagiannya, maka perlu mengeliminasi x derajat 3 & 2;
(x2-4)(2x+a) = 2x3+ax2-8-4a
Lalu lakukan eliminasi sehingga;
2x3+ax2-bx+3
2x3+ax2-8-4a
————— –
(8-b)x+(3+4a);
(8-b)x+(3+4a) mempunyai kesamaan dengan x+23;
8-b = 1 -> b = 8-1 = 7
3+4a = 23 -> a = 20/4 = 5
Hasil akhirnya menjadi
a-b = 5-7 = -2
Contoh Soal (2)
Apabila diketahui
f(x) = px2+qx-3
g(x) = 3(x+1)(x-1)
serta f(x)=g(x)!
Carilah nilai p+q!
A. 3
B. 0
C. -3
D. 1
Jawaban : A. 3
Pembahasan :
Ubah lebih dulu g(x) sehingga;
g(x) = 3x2-3; kemudian langsung ke bentuk kesamaan
px2+qx-3 = 3x2-3
px2+qx-3 = 3x2-(0)x-3
Maka p=3 & q=0
Jadi p+q = 3+0 = 3
Contoh Soal (3)
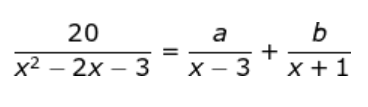
Carilah masing-masing nilai a & b berdasarkan soal di atas!
A. a=5 & b=5
B. a=-5 & b=-5
C. a=5 & b=-5
D. a=-5 & b=5
Jawaban : C. a=5 & b=-5
Pembahasan :
- Menggunakan Cara Pertama (subtitusi & eliminasi)
Karena x2-2x-3 = (x-3)(x+1) maka;
a dikalikan (x+1)
b dikalikan (x-3)
Sehingga bentuknya menjadi :
(ax+a)+(bx-3b) = 20
(a+b)x+(a-3b) = (0)x+20 -> kesamaan suku banyak
(a+b) = 0 -> a=-b
(a-3b) = 20 -> (-b-3b) = 20 -> b = 20/(-4) = -5
Sedangkan a=-b -> a = 5
Jadi a=5 & b=-5
- Menggunakan Cara Kedua (mengalikan akarnya)
Setelah menyamakan penyebutnya sehingga
[a(x+1)] + [b(x-3)] = 20 ;
Ketika x=-1
[a(x+1)] + [b(x-3)] = 20
[a(0)] + [b(-4)] = 20
b = 20/(-4) = -5
Ketika x=3
[a(x+1)] + [b(x-3)] = 20
[a(4)] + [b(0)] = 20
a = 20/4 = 5
Contoh Soal (4)
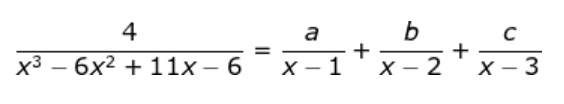
Jika Nami mempunyai persamaan seperti di atas, tentukan hasil penjumlahan a+b+c nya!
A. 3
B. 2
C. 1
D. 0
Jawaban : D. 0
Pembahasan :
Karena persamaannya mempunyai derajat 3, langsung saja gunakan cara perkalian akar;
4 = [a(x-2)(x-3)] +[b(x-1)(x-3)] +[c(x-1)(x-2)]
- Saat x=1 nilai b & c adalah 0, sementara
[a(x-2)(x-3)] = 4
[a(1-2)(1-3)] = 4
2a = 4
a = 2 - Saat x=2 nilai a & c adalah 0, sementara
[b(x-1)(x-3)] = 4
[b(2-1)(2-3)] = 4
-b = 4
b = -4 - Saat x=3 nilai a & b adalah 0, sementara
[c(x-1)(x-2)] = 4
[c(3-1)(3-2)] = 4
2c = 4
c = 2
Sehingga hasil dari a+b+c = 2+(-4)+2 = 0
Contoh Soal (5)
4x3+4x2+(2a-2b)x+(bc) = 0
2x3+(a+b)x2+12 = 0
Apabila kedua persamaan di atas memiliki kesamaan suku banyak, berapakah (a-b+c)?
A. 24
B. 12
C. 6
D. 3
Jawaban : A. 12
Pembahasan :
Pertama setarakan terlebih dulu;
4x3+4x2+(2a-2b)x+(bc) = 0
4x3+(2a+2b)x2+(0)x+24 = 0
Lalu lanjutkan proses eliminasi;
(2a+2b) = 4
(2a-2b) = 0
————- –
4b = 4
b = 1
Kemudian;
2a+2b = 4
2a+2=4
a= (4-2)/2 = 1
Kemudian;
(bc) = 24
c = 24/b = 24/1 = 24
Sehingga (a-b+c) = 1-1+24 = 24
Akhir Kata
Demikian uraian Kursiguru mengenai contoh soal kesamaan suku banyak pada pelajaran matematika kelas 11 SMA. Semoga dengan adanya pembahasan contoh soal kesamaan suku banyak di atas mampu memudahkan para pelajar dalam mengerjakan tugas, ulangan harian ataupun ujian lainnya.

