Contoh Soal Persamaan Kuadrat Kelas 9 – akan membahas mengenai contoh soal yang akan muncul ketika seorang siswa kelas 9 mempelajari mata pelajaran matematika, khususnya materi persamaan kuadrat. Dimana bila dilihat dari garis besarnya, persamaan kuadrat merupakan salah satu bentuk aljabar.
Persamaan kuadrat mempunyai pengertian sebagai sebuah persamaan dimana nilai ordo terbesar adalah 2 (dua). Artinya ketika mempelajari persamaan kuadrat, siswa hanya akan menemukan persamaan simpel seperti salah satu contohnya adalah x2+2x+2.
Tak berbeda jauh dari ilmu matematika lain, persamaan kuadrat kelas 9 juga memiliki beberapa cara penyelesaian, rumus khusus dan harus dipelajari melalui contoh soal. Oleh karena itu, sudah seharusnya pelajar kelas 3 SMP dan MTs mempelajari contoh soal persamaan kuadrat.
Pada kesempatan kali ini, Kursiguru akan memberikan penjelasan mengenai ringkasan materi, rumus dan contoh soal persamaan kuadrat beserta jawabannya. Selain itu, penulis juga akan membagikan file contoh soal persamaan kuadrat PDF yang bisa didownload.
Ringkasan Materi Persamaan Kuadrat
Bahasan kali ini akan penulis awali dari penjelasan singkat mengenai ringkasan materi persamaan kuadrat. Jika dilihat secara seksama, persamaan kuadrat adalah bentuk aljabar dengan satu atau 2 variabel serta sebuah konstanta. Seperti telah disinggung di atas, hal ini disebabkan karena persamaan kuadrat hanya memiliki ordo 2.
Contoh sederhana persamaan kuadrat :
- x2-3x+4
- 4x2-4x+4
Dari kedua contoh di atas, bisa diketahui bahwa persamaan kuadrat dapat dituliskan sebagai ax2+bx+c dengan a, b maupun c bisa bernilai positif ataupun negatif.
Sebuah persamaan kuadrat dengan bentuk ax2+bx+c = 0 juga mempunyai komponen lain yakni Diskriminan (D). Dimana besarnya diskriminan dapat dicari melalui konstanta a, b, c yaitu menggunakan ketentuan D=b2-4ac.
Jika ditinjau dari nilai (D), akar sebuah persamaan kuadrat dapat langsung diketahui jenisnya.
- Apabila besaran (D)<0, maka akar persamaan kuadrat tidak real (imajiner).
- Apabila besaran (D)>0, maka akar persamaan kuadrat nilainya real serta x1 dan x2 tidaklah sama.
- Apabila besaran (D)=0, maka akar persamaan kuadrat nilainya real serta x1=x2.
Rumus Persamaan Kuadrat
Setelah memahami penjelasan di atas, selanjutnya kamu perlu mengetahui rumus mudah dalam mencari akar sebuah soal persamaan kuadrat. Dimana setidaknya ada 2 (dua) rumus mudah dalam mencari hasil contoh soal persamaan kuadrat kelas 9, yaitu:
1. Rumus Pemfaktoran
Untuk mengetahui rumus pemfaktoran soal persamaan kuadrat, silakan simak langsung tabel di bawah ini.
| Syarat | Model Persamaan | Pemfaktoran | Ketentuan | Akar Hasil |
|---|---|---|---|---|
| a = 1 | x2+bx+c = 0 | (x+p)(x+q) =0 | p+q=b p.q=c | x1=-p x2=-q |
| a≠0 a≠1 | ax2+bx+c = 0 | 1/a (ax+p)(ax+q) = 0 | p+q=b p.q=a.c | x1=-p x2=-q/a |
| c=0 | ax2+bx = 0 | x(ax+b) = 0 | x1=0 x2=-b/a |
2. Rumus abc
Seperti halnya metode pemfaktoran di atas, nilai abc serta D pada persamaan kuadrat juga dapat digunakan dalam rumus lain sebagai berikut.

Contoh Soal Persamaan Kuadrat Kelas 9
Jika sudah paham mengenai rumus persamaan kuadrat di atas, maka silakan coba pahami cara menyelesaikan sebuah soal persamaan kuadrat dari beberapa contoh persoalan di bawah ini.
Contoh Soal Persamaan Kuadrat (1)

Contoh Soal Persamaan Kuadrat (2)
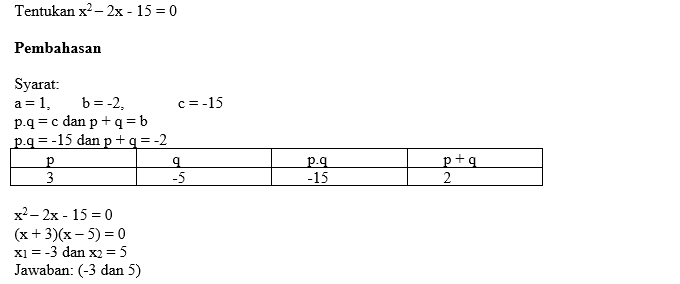
Contoh Soal Persamaan Kuadrat (3)

Perlu diketahui juga bahwa terkadang bentuk persamaan kuadrat seperti di atas tersebut muncul dalam Contoh Soal AKM SMP, maka kamu harus benar-benar menguasainya.
Download Contoh Soal Persamaan Kuadrat
Untuk melengkapi pembahasan terkait persamaan kuadrat kelas 9 kali ini, penulis juga akan membagikan sebuah file PDF berisi kumpulan soal yang bisa kamu gunakan untuk belajar secara mandiri ataupun sebagai bahan mengajar di kelas.
Akhir Kata
Dari seluruh pembahasan di atas, kesimpulan utama untuk memahami ilmu seputar persamaan kuadrat adalah berlatih melalui contoh soal secara terus menerus. Sehingga baik rumus ataupun ketentuan akan tertanam pada ingatan siswa siswi kelas 9 SMP dan MTs.

